Appariement par score de propension (PSM) : mise en oeuvre avec R et discussions méthodologiques
Pour évaluer un effet causal, comme par exemple les effets d'un médicament sur des patients, on a besoin de ce que l'on appelle un essai clinique randomisé. Le principe est le suivant : on prend un certain nombre de patients (à déterminer en fonction de l'effet minimum attendu, mais c'est un autre sujet) et on les sépare aléatoirement en deux groupes : un groupe traitement qui prend le médicament et un groupe contrôle qui en général prend un placebo.
Comme on a décidé de manière complètement aléatoire l'assignation à l'un ou l'autre groupe, on sait que ces deux groupes auront en moyenne des caractéristiques identiques (merci la loi faible des grands nombres!). Cela nous permet de conclure que les différences qui seraient observées entre les deux groupes (meilleur rétablissement, prise de poids, selon ce qu'on cherche à observer...) sont imputables au traitement et non à une spécificité d'un des groupes par rapport à l'autre.
L'essai clinique randomisé, c'est donc l'idéal pour montrer un effet causal et c'est d'ailleurs par là qu'il faut passer si vous souhaitez homologuer un nouveau médicament. Mais c'est également coûteux et difficile à réaliser. C'est pourquoi on cherche de plus en plus à essayer d'imiter les conditions d'un essai clinique randomisé à partir de données observationnelles. Pour cette note de blog, on va vous présenter une ces méthodes : le propensity score matching (PSM), ou appariement par score de propension.
Principes du Propensity Score Matching
L'appariement par score de propension vise à recréer les conditions d'un essai clinique à partir de données observationnelles. On a ainsi un ensemble de données avec par exemple un certain nombre de patients qui ont pris un traitement (le groupe traitement) et d'autres qui ne l'ont pas pris (le groupe contrôle). Problème : ces population qui n'ont pas été séparées de manière aléatoire peuvent être très différentes et il n'est pas possible en l'état de conclure qu'une différence entre elles soit imputable au traitement en question. Il faut donc recréer deux groupes de contrôle et de traitement qui puissent être comparables.
Calcul du score de propension
La première étape est de calculer le score de propension. Il est nécessaire en premier lieu d'identifier les variables observables sur lesquelles on souhaiterait rééquilibrer les deux groupes. Il n'y a pas de méthode magique pour choisir ces variables : il faut que ce soit la connaissance technique du cas qui guide votre choix. L'idée est d'identifier les variables dont vous imaginez qu'elles peuvent être déséquilibrées entre vos deux groupes pour différentes raisons (par exemple, le traitement A est plus souvent donné aux femmes donc je sais qu'il y aura plus de femmes dans ce groupe que dans un autre). Il faut aussi bien sûr contrôler par les variables dont on sait qu'elles peuvent avoir un impact sur le résultat indépendemment de l'efficacité du médicament (l'âge impacte souvent la probabilité de guérison par exemple).
Une fois ces variables identifiées, il ne vous reste plus qu'à faire sur l'ensemble de vos données un modèle de régression logistique. Par exemple, si votre groupe traitement prend un médicament A et le reste du groupe ne prend pas ce médicament, votre variable Y sera l'indicatrice Prend le médicament A et vos variables \(X_i\) les variables sur lesquelles vous souhaitez contrôler (sexe, âge, etc...). La formule est la suivante :
\(\log \left( \frac{P(Y=1)}{1 - P(Y=1)} \right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \dots\)
Appariement de vos données
La mise en oeuvre de cette régression logistique nous permet d'obtenir un score de propension. Celui-ci représente pour chaque individu la probabilité prédite qu'il appartienne au groupe traitement. Ce score de propension peut-être utilisé dans différentes méthodes (IPTW, variable d'ajustement dans la modèle...). Pour le PSM, nous l'utilisons pour apparier les données.
En effet, pour chaque observation du groupe traité, l'idée est de lui attribuer une (ou plusieurs, selon vos données) observation(s) du groupe contrôle, ayant un score de propension le plus proche possible, donc des caractéristiques semblables. Différentes méthodes d'appariement existent, la plus courante étant celle du plus proche voisin.
Une fois que chaque observation du groupe traitement s'est vue attribuer son plus proche voisin du groupe contrôle, on écarte les données qui n'ont pas été appariées. La première chose à faire est bien sûr d'évaluer la qualité de l'appariement en vérifiant la répartition des variables de contrôle entre les deux groupes. Puis, nous allons réaliser nos analyses comme si nous étions dans le cas d'un essai clinique randomisé, ou presque...
👋 Nous c'est Antoine et Louis de Statoscop, une coopérative de statisticiens / data scientists. Vous voulez en savoir plus sur ce que l'on fait?
Mise en oeuvre de l'appariement par score de propension avec R
Les méthodes utilisant des scores de propension, et en particulier l'appariement par score de propension, sont très bien prises en charge avec R. Nous vous proposons ici d'utiliser le package R MatchIt sur des données cliniques librement accessibles. Il s'agit de patients hospitalisés pour une insuffisance cardiaque.
Description des données et de notre problématique
Nos données représentent 299 patients. Parmi eux, la prévalence de cas d'hypertension artérielle (HTA) est la suivante :
Table: Présence de diabètes
| high_blood_pressure | n |
|---|---|
| Non | 194 |
| Oui | 105 |
Il y a 13 variables disponibles :
## [1] "age" "anaemia"
## [3] "creatinine_phosphokinase" "diabetes"
## [5] "ejection_fraction" "high_blood_pressure"
## [7] "platelets" "serum_creatinine"
## [9] "serum_sodium" "sex"
## [11] "smoking" "time"
## [13] "death_event"
On cherche ici à évaluer l'impact de l'HTA sur la probabilité de décéder des suites d'une insuffisance cardiaque. Notre variable d'intérêt est donc death_event. Notre traitement (ici on ne regarde pas l'effet d'un traitement mais d'une caractéristique des patients, cependant on va continuer à utiliser cette terminologie) est ici le fait d'avoir une HTA. Le croisement de ces deux variables donne le résultat suivant :
Table: HTA et décès
| high_blood_pressure | Effectifs | Part de décès |
|---|---|---|
| Non | 194 | 0.29 |
| Oui | 105 | 0.37 |
Ici à première vue on trouve une proportion plus importante de décès parmi les patients ayant une HTA (37% contre 29% pour les autres). Mais bien sûr, il n'est pas encore possible de savoir si cela est dû à l'HTA en soi ou à d'autres caractéristiques des patients souffrant de ce problème.
Calcul du score de propension et appariement des patients
La fonction matchit du package R MatchIt nous permet de mettre directement en oeuvre le calcul du score de propension et l'appariement. On commence par sélectionner les variables par lesquelles il nous semble important de contrôler : ici nous allons prendre l'ensemble des variables cliniques dont nous disposons. Il faut alors retirer les valeurs manquantes pour ensuite obtenir deux groupes de patients avec et sans HTA ayant des caractéristiques semblables par ailleurs. La fonction s'écrit ainsi :
library(MatchIt)
m.out1 <- matchit(high_blood_pressure ~ age + sex + anaemia + creatinine_phosphokinase + diabetes +
platelets + serum_creatinine + serum_sodium + smoking,
data = data_ps,
method = "nearest",
distance = "glm",
estimand = "ATT")
Ici on choisit le paramétrage par défaut method = "nearest" qui apparie à chaque observation du groupe traité (les patients ayant une HTA) l'observation du groupe contrôle ayant le score de propension le plus proche possible.
Le paramètre method = "ATT" permet d'évaluer un effet du traitement sur les traités et non sur la population globale. Enfin, on définit le modèle (ici logistique avec avec distance = "glm") pour le calcul du score de propension. Si vous avez un doute sur la méthode à utiliser, reportez-vous à la documentation du package MatchIT.
Évaluation de la qualité de l'appariement
Encore une fois, la librairie MatchIt nous mâche directement le travail en nous permettant de comparer facilement la répartition de nos patients avant et après appariement avec summary(). La répartition avant l'appariement est la suivante :
output_matching <- summary(m.out1)
# on affiche seulemet l'élément `sum.all` de la sortie
output_matching$sum.all |>
knitr::kable(digits = 2)
| Means Treated | Means Control | Std. Mean Diff. | Var. Ratio | eCDF Mean | eCDF Max | Std. Pair Dist. | |
|---|---|---|---|---|---|---|---|
| distance | 0.37 | 0.34 | 0.36 | 1.01 | 0.11 | 0.23 | NA |
| age | 62.34 | 60.02 | 0.20 | 0.91 | 0.06 | 0.13 | NA |
| sexFemme | 0.42 | 0.31 | 0.21 | NA | 0.10 | 0.10 | NA |
| sexHomme | 0.58 | 0.69 | -0.21 | NA | 0.10 | 0.10 | NA |
| anaemiaNon | 0.54 | 0.58 | -0.08 | NA | 0.04 | 0.04 | NA |
| anaemiaOui | 0.46 | 0.42 | 0.08 | NA | 0.04 | 0.04 | NA |
| creatinine_phosphokinase | 488.90 | 632.14 | -0.16 | 0.73 | 0.05 | 0.11 | NA |
| diabetesNon | 0.59 | 0.58 | 0.03 | NA | 0.01 | 0.01 | NA |
| diabetesOui | 0.41 | 0.42 | -0.03 | NA | 0.01 | 0.01 | NA |
| platelets | 269989.18 | 259769.00 | 0.12 | 0.66 | 0.04 | 0.10 | NA |
| serum_creatinine | 1.39 | 1.40 | -0.01 | 1.99 | 0.03 | 0.13 | NA |
| serum_sodium | 136.85 | 136.51 | 0.08 | 0.82 | 0.01 | 0.05 | NA |
| smokingNon | 0.71 | 0.66 | 0.12 | NA | 0.05 | 0.05 | NA |
| smokingOui | 0.29 | 0.34 | -0.12 | NA | 0.05 | 0.05 | NA |
On constate ainsi que les personnes souffrant d'hyper tension artérielle sont souvent plus âgées que les autres. Ce sont également plus souvent des femmes, et plus souvent des personnes atteintes d'anémie. Observons maintenant si notre appariement a permis d'équilibrer nos deux groupes sur ces variables et sur les autres :
# on affiche seulement l'élément `sum.matched` de la sortie
output_matching$sum.matched |>
knitr::kable(digits = 2)
| Means Treated | Means Control | Std. Mean Diff. | Var. Ratio | eCDF Mean | eCDF Max | Std. Pair Dist. | |
|---|---|---|---|---|---|---|---|
| distance | 0.37 | 0.37 | 0.04 | 1.10 | 0.01 | 0.10 | 0.05 |
| age | 62.34 | 62.36 | 0.00 | 0.93 | 0.03 | 0.07 | 0.89 |
| sexFemme | 0.42 | 0.40 | 0.04 | NA | 0.02 | 0.02 | 0.54 |
| sexHomme | 0.58 | 0.60 | -0.04 | NA | 0.02 | 0.02 | 0.54 |
| anaemiaNon | 0.54 | 0.56 | -0.04 | NA | 0.02 | 0.02 | 0.96 |
| anaemiaOui | 0.46 | 0.44 | 0.04 | NA | 0.02 | 0.02 | 0.96 |
| creatinine_phosphokinase | 488.90 | 481.78 | 0.01 | 0.89 | 0.02 | 0.07 | 0.46 |
| diabetesNon | 0.59 | 0.63 | -0.08 | NA | 0.04 | 0.04 | 1.01 |
| diabetesOui | 0.41 | 0.37 | 0.08 | NA | 0.04 | 0.04 | 1.01 |
| platelets | 269989.18 | 264619.41 | 0.06 | 0.87 | 0.03 | 0.10 | 1.02 |
| serum_creatinine | 1.39 | 1.43 | -0.03 | 2.09 | 0.04 | 0.18 | 0.66 |
| serum_sodium | 136.85 | 136.60 | 0.06 | 0.88 | 0.01 | 0.05 | 1.07 |
| smokingNon | 0.71 | 0.74 | -0.06 | NA | 0.03 | 0.03 | 0.74 |
| smokingOui | 0.29 | 0.26 | 0.06 | NA | 0.03 | 0.03 | 0.74 |
On constate que la plupart des variables sont maintenant plus équilibrées entre les deux groupes. Au global, la variable distance montre la grande proximité du score de propension entre les deux groupes. On peut également mettre en évidence l'effet de l'appariement visuellement sur quelques unes des variables avec la fonction plot : |
plot(m.out1, type = "density", interactive = FALSE,
which.xs = ~ age + anaemia + sex)
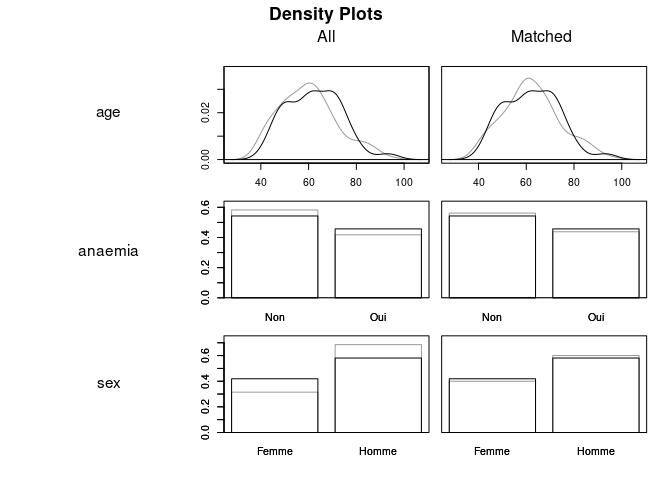
Mesure des effets causaux à partir de la population appariée
Une fois convaincus de la qualité de l'appariement, on peut mettre en oeuvre notre modèle statistique en tenant compte pour le calcul des estimateurs du fait que nous manipulons des observations appariées. Différentes méthodes sont possibles en fonction de la variable d'intérêt, du type d'appariement réalisé, etc. En cas de doute, vous pouvez vous reporter à la vignette consacrée à l'estimation des effets du package MatchIt.
Dans notre exemple simple, nous allons tout d'abord extraire les données appariées avec match_data et calibrer un modèle linéaire généralisé. Nous pondérons avec les poids issus de l'appariement. S'ils sont tous égaux à 1 (c'est le cas pour nous) cela n'est pas nécessaire. Toutefois, cela reste une bonne habitude en cas d'appariement utilisant des poids différents. Il est possible également de contrôler notre régression logistique par les variables ayant servi à l'appariement, ou directement par le score de propension. Nous choisissons ici de ne pas le faire en raison de la bonne qualité de l'appariement.
Enfin, on utilise le package marginaleffects pour estimer l'effet moyen sur les traités (ATT) en tenant compte l'appariement.
data_matched <- match_data(m.out1)
fit <- glm(death_event ~ high_blood_pressure,
data = data_matched,
family = binomial,
weights = weights)
results <- marginaleffects::avg_comparisons(fit,
vcov = ~subclass,
newdata = subset(high_blood_pressure == "Oui"))
print(results) |>
knitr::kable(digits=2)
| term | contrast | estimate | std.error | statistic | p.value | s.value | conf.low | conf.high | predicted_lo | predicted_hi | predicted |
|---|---|---|---|---|---|---|---|---|---|---|---|
| high_blood_pressure | Oui - Non | 0.05 | 0.06 | 0.76 | 0.45 | 1.16 | -0.08 | 0.17 | 0.32 | 0.37 | 0.37 |
L'estimateur représente la différence de proportions de décès entre le groupe traité (ceux avec HTA) et le groupe contrôle (les autres). Elle est ici de 0.05, soit 5 points de pourcentage. En effet, les variables predicted_lo et predicted_hi indiquent que lorsqu'on apparie, la part de décès dans le groupe contrôle monte à 32% (contre 29% dans l'ensemble des patients n'ayant pas de tension artérielle), alors qu'elle est de 37% dans le groupe traité. De fait, cette différence n'est pas significative, puisque la p-value est de 0.45 (un autre de nos articles explique ce qu'est une p-value). Bien sûr, cela ne signifie pas forcément que cet effet n'existe pas, mais en tout cas on ne dispose pas dans nos données de suffisament d'observations pour affirmer ici que l'HTA augmente signficativement la probabilité de décès.
Forces et limites des méthodes avec score de propension
De nombreuses questions se posent autour des méthodes de score de propension. La première est sans doute son avantage réel ou supposé par rapport à un modèle multivarié classique. Il est vrai cependant que cette méthode a l'avantage de capter dans une seule variable un ensemble de dimensions observables par lesquelles on souhaite contrôler notre analyse. Mais le fait, dans le cas de l'appariement, de se passer d'une partie des données pose question. Cela permet cependant de calculer un effet moyen sur les traités (ATT) et de ne pas trop biaiser l'effet avec des observations qui auraient des caractéristiques très éloignées de la population traitée. De plus, la méthode de pondération par inverse de probabilité de traitement (IPTW) permet d'utiliser le score de propension sans écarter de données, et il est également possible d'estimer un ATT.
La plus grosse limite de cette méthode est sans doute le fait qu'elle pourrait faire oublier que nos groupes de traitement et de contrôle sont comparables uniquement sur des caractéristiques observables. Il n'est donc pas à exclure que des biais de sélection non observables polluent notre analyse, là où un essai clinique randomisé calibré correctement met normalement à l'abri de ce problème. Il est donc fondamental de garder constamment cet écueil en tête pour essayer d'anticiper les possibles défauts de nos analyses.
C'est tout pour aujourd'hui! Si vous cherchez des statisticiens pour vos études cliniques n'hésitez pas à visiter notre site et à nous suivre sur Twitter et Linkedin. Pour retrouver le code ayant servi à générer cette note, vous pouvez vous rendre sur le github de Statoscop.