Comprendre et interpréter les p-values

Aujourd'hui c'est à un grand classique de la statistique que l'on s'attaque : la p-value, ou valeur p. Fondamentale dans l'analyse des résultats de la recherche scientifique, elle est pourtant souvent mal interprétée. C'est sur elle que l'on s'appuie pour confirmer ou infirmer une hypothèse et juger de la significativé de nos résultats. Mais qu'est-ce que cela implique et comment bien appréhender ce qu'elle permet (et surtout ce qu'elle ne permet pas) de conclure? On essaye de voir ça ensemble, de la manière la plus intuitive possible!

Les p-values et les tests statistiques

Pour comprendre les p-values, il faut aborder la notion de tests statistiques. Ils permettent de tester une Hypothèse nulle H0 contre une hypothèse alternative H1. Par exemple, prenons le cas d'une régression linéaire où on cherche à estimer des coefficients \(\beta_i\) décrivant le lien entre une variable d'intérêt \(Y\) et des variables explicatives \(X_i\) :

\(Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \dots\)

Pour chaque coefficient estimé \(\beta_i\), on utilise le test t de Student qui nous permet de tester les hypothèses :
- H0 : \(\beta_i = 0\)
- H1 : \(\beta_i \neq 0\)

Le principe du test est le suivant : on va partir du principe que H0 est vrai et on va voir quelle est la chance d'observer notre résultat dans ce monde théorique. Ce test statistique va ainsi nous donner la distribution possible des résultats que l'on pourrait obtenir à partir de différents échantillons si H0 était vraie. Selon où l'on se situe dans cette distribution, on va pouvoir juger de la vraisemblance de cette hypothèse H0, en fonction d'un seuil alpha que l'on peut faire varier. En fonction de la valeur de t obtenue avec notre échantillon, on peut décider de rejeter ou non l'hypothèse H0 :

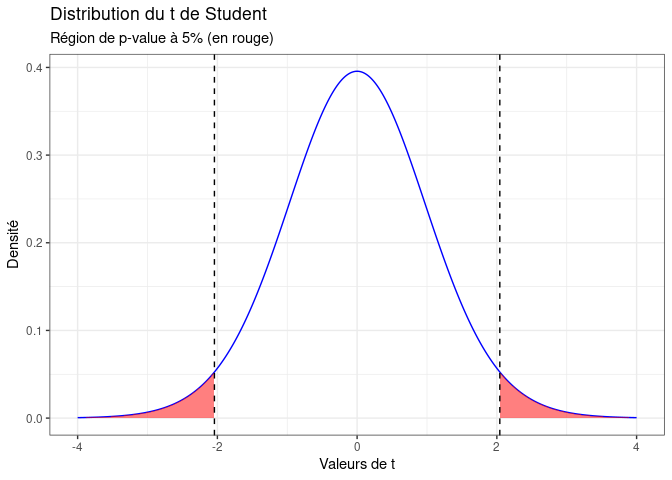
Sur le graphique ci-dessus, la zone rouge représente 5% de l'aire de la courbe de densité. Si la valeur obtenue par notre test est dans cette zone, on sait que cela représenterait 5% ou moins des résultats possibles que l'on aurait obtenus si H0 était vraie. On peut donc en déduire que la nullité du coefficient est peu probable.

Bien sûr, si on modifie le seuil alpha dans un sens plus restrictif, mettant le seuil de significativité à 1%, cela va restreindre la zone rouge de notre graphique. Il faudra alors obtenir une valeur t encore plus extrême pour rejeter H0 :

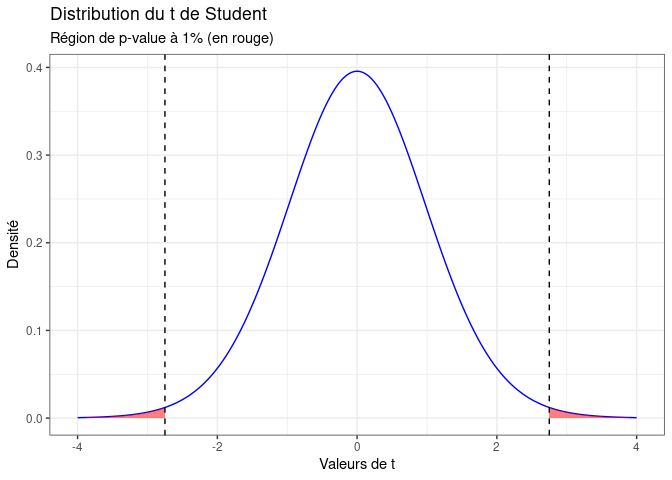
Ainsi, lorsqu'on fait tourner un modèle de régression sur notre logiciel de statistiques favori et que l'on obtient une p-value, il s'agit du seuil alpha de notre hypothèse H0 qui doit nous permettre de décider de la rejeter ou non. On va donc l'utiliser pour décider de la significativité de ce coefficient. Si l'on devait synthétiser ce que veut dire la p-value en une phrase, cela donnerait :

Si la vraie valeur du coefficient était 0 et que j'avais fait tourner ce modèle sur 100 échantillons différents, j'aurais obtenu un résultat au moins aussi extrême dans p cas.

Ainsi, plus p est faible, plus on peut écarter l'hypothèse que le coefficient estimé soit nul.

Interprétation des p-values

Il faut bien comprendre que la p-value et la significativité du coefficient qui en découle ne portent que sur la question de savoir si ce coefficient est ou non différent de zéro. Cela n'indique pas si le résultat trouvé a une importance particulière. Un coefficient peut très bien être significatif statistiquement (donc probablement différent de zéro) mais en pratique insignifiant. Il faut donc le confronter à l'expertise pratique de la question de recherche étudiée.

Une faible p-value n'est pas non plus le signe d'une estimation précise. Pour juger de cet aspect, il est important de regarder les intervalles de confiance. Un coefficient peut très bien être significativement différent de zéro mais avoir un intervalle de confiance très large, ce qui est très important à considérer en fonction des implications pratiques de votre recherche. On sait seulement que si par exemple l'intervalle de confiance à 95% ne contient pas 0 (ou 1 si on estime des odds-ratios), le coefficient estimé est significatif à au moins 5%.

De plus, un résultat peut être non significatif en raison d'une mauvaise calibration du modèle : un échantillon trop peu important, de trop nombreuses variables explicatives, etc... C'est notamment pour cette raison qu'il ne faut pas directement interpréter un coefficient non significatif comme un absence d'effet. C'est plutôt une absence de preuve d'effet. Oui, c'est moins facile à rédiger, mais cela rend plus justice à la complexité des statistiques inférentielles.

En général, le consensus scientifique fixe le seuil de significativité à 5%. Bien sûr, c'est forcément au moins partiellement arbitraire et cela pose question : on écarterait un résultat avec une p-value à 5,1% mais on afficherait fièrement celui avec une p-value à 4,9%?

Il est ainsi tentant pour les chercheurs de construire leur modèle en fonction de la p-value recherchée, et non de la question de recherche affichée, ce qui est complètement contre-productif. D'autant que la nature de la p-value fait que si l'on teste un nombre très important de fois, on finira bien par trouver des résultats significatifs, mais uniquement du fait du hasard. Cette mauvaise pratique, volontaire ou non, est bien identifiée et se nomme le p-hacking. La bonne manière de se prémunir de cet écueil est de définir la question de recherche et les modèles statistiques en amont de la collecte de données et de calibrer l'échantillon en fonction de ceux-ci. Il faut ensuite tâcher de ne pas s'écarter de ces axes de recherche...même si on n'obtient pas les p-values qu'on espérait!

Conclusion

La p-value, ça n'est donc pas du tout la probabilité que le coefficient soit incorrect ! Dans le cas d'une régression, c'est un indicateur de la vraisemblance que celui-ci soit égal à zéro. Mais un coefficient significatif peut aussi avoir une estimation très imprécise, ou une valeur insignifiante. Il est donc fondamental d'affiner son diagnostic, avec par exemple les intervalles de confiance, et surtout l'interprétation de quelqu'un qui comprend les implications pratiques d'un coefficient!

C'est tout pour aujourd'hui! N'hésitez pas à visiter notre site (qui a fait peau neuve, vous avez remarqué?) et à nous suivre sur Twitter et Linkedin. Pour retrouver le code ayant servi à générer cette note, vous pouvez vous rendre sur le github de Statoscop.