Réseaux neuronaux convolutifs avec R et Keras
On le sait, le débat entre R et Python est acharné et souvent peu productif. En Machine Learning, tout le monde ou presque s'accorde à dire que Python a une longueur d'avance, surtout pour les modèles de Deep Learning (réseaux de neurones).
Heureusement, il existe souvent des alternatives pour celles et ceux ne souhaitant pas se mettre à un autre langage (même si on vous y encourage!). Ainsi le package R keras3 permet d'accéder à la célèbre API Python du même nom. Nous vous montrons donc dans cet article comment elle fonctionne.
Présentation de la librairie Keras
Origine de la librairie
Keras est une API Python qui permet de créer et entraîner des modèles de Deep Learning. Elle a l'avantage d'offrir une interface simple et une syntaxe claire. Elle permet également d'accéder à de nombreux modèles pré-entraînés qui peuvent ensuite facilement être fine-tunés sur d'autres données. Elle a été récemment intégrée à TensorFlow mais peut s'appuyer sur d'autres backends.
Keras dispose aussi d'une documentation très complète, et sa popularité permet de retrouver de nombreux exemples d'utilisation en ligne. Elle est le plus souvent utilisée grâce au package Python keras ou via TensorFlow avec tf.keras, qui permettent d'exploiter facilement ses différentes méthodes.
Installation du package sur R
Grâce notamment à la puissance de reticulate, un package permettant de faire tourner Python depuis une session R, on dispose maintenant d'un package R keras, que nous vous présentons ici. Nous utiliserons la dernière version disponible, le package keras3. La première étape est bien sur d'installer le package avec install.packages("keras3") puis de lancer la fonction keras3::install_keras() qui permet d'installer Python et un environnement anaconda dédié.
library(keras3)
install_keras()
Si vous avez du GPU, vous pouvez vérifier que votre device a bien été repéré avec l'instruction suivante (normalement, tensorflow a été installé au moment de l'installation de keras3) :
tensorflow::tf$config$list_physical_devices("GPU")
## [[1]]
## PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')
👋 Nous c'est Antoine et Louis de Statoscop, une coopérative de statisticiens / data scientists. Vous voulez en savoir plus sur ce que l'on fait?
Entraîner un premier réseau convolutionnel
Pour notre petite démonstration, nous allons utiliser la célébrissime base de données mnist qui contient des images de chiffres écrits à la main. Le but est donc de développer un modèle capable de reconnaître les chiffres manuscrits.
Pré-traiter vos données
Les données fournies contiennent 60 000 observations pour les données d'entraînements et 10 000 pour les données de test. Les images étant renseignées directement sous forme de matrice dans le package keras3 nous n'avons besoin que de normaliser ces matrices sur [0, 1]. On passe aussi la variable d'intérêt, qui donne la valeur du chiffre en question, sous un one-hot-encoder avec la fonction to_categorical. On obtient ainsi un vecteur de taille 10 contenant un indicateur pour chaque chiffre.
library(keras3)
mnist <- dataset_mnist()
x_train <- mnist$train$x
y_train <- mnist$train$y
x_test<- mnist$test$x
y_test <- mnist$test$y
# on normalise sur [0, 1]
x_train <- x_train/255
x_test <- x_test/255
# one-hot-encoder pour la variable d'intérêt avec to_categorical
y_train <- to_categorical(y_train, num_classes = 10)
y_test <- to_categorical(y_test, num_classes = 10)
Initialiser et définir votre réseau de neurones profond
On initialise le modèle avec keras_model_sequential, dans lequel on précise d'emblée la dimension des données que le modèle prendra en entrée. Puis on ajoute les différentes couches de neurones.
Comme nous sommes dans un réseau convolutionnel, on commence directement par une couche de convolution, qui permet de faire ressortir les caractéristiques de chaque image. Cela fonctionne grâce à un système de filtres, réalisé en faisant le produit de la matrice de pixels et d'une matrice plus petite, appelée feature detector. On définit dans cette étape le nombre de filtres que l'on souhaite faire passer avec le paramètre filters et la taille de la matrice feature detector avec le paramètre kernel_size.
On applique ensuite aux matrices obtenues une couche de max pooling qui permet de réduire les dimensions du problème en ne conservant que les valeurs les plus importantes. Cette étape permet aussi de rendre plus souvent comparables des images ayant des caractéristiques semblables à des endroits différents. Le paramètre pool_size permet de choisir la taille du sous-ensemble sur lequel on ne va garder que la valeur maximale.
On peut ensuite refaire des nouvelles couches de convolution suivies de pooling, en fonction de la complexité et de la taille de nos matrices de pixel en entrée du modèle. On termine ces étapes par une couche flatten() qui permet d'obtenir un vecteur unidimensionnel pour chaque observation, sur lequel on va pouvoir construire notre réseau de neurones profond avec des couches dense(). On choisit ici une couche avec 128 neurones, suivie d'une couche avec 64 neurones. La couche de sortie contient 10 neurones correspondant aux 10 classes possibles.
Le package R keras3 permet une syntaxe très proche de celle que l'on utiliserait sur Python. On peut en plus relier ces couches avec l'opérateur |>, rendant le code encore plus lisible et aéré. À noter qu'une fois que le modèle my_first_r_cnn est créé, il n'est pas nécessaire de le réassigner à chaque ajout de layers. L'opérateur |> met à jour directement l'objet my_first_r_cnn.
# Initialisation du modèle
my_first_r_cnn <- keras_model_sequential(input_shape = c(28,28,1))
# convolution et max pooling
my_first_r_cnn |>
# on définit les dimension des inputs dans une couche dédiée
layer_conv_2d(filters = 32, kernel_size = c(3, 3),
# l'activation relu "casse" une linéarité qui a pu
# être introduite avec la convolution
activation = 'relu') |>
layer_max_pooling_2d(pool_size = c(2, 2)) |>
layer_conv_2d(filters = 16, kernel_size = c(2, 2),
activation = 'relu') |>
layer_max_pooling_2d(pool_size = c(2, 2)) |>
layer_flatten() |>
layer_dense(units = 128, activation = 'relu') |>
layer_dense(units = 64, activation = 'relu') |>
layer_dense(units = 10, activation = 'softmax')
On peut illustrer la structure de notre modèle avec la fonction summary() :
summary(my_first_r_cnn)
## Model: "sequential"
## ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
## ┃ Layer (type) ┃ Output Shape ┃ Param # ┃
## ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
## │ conv2d (Conv2D) │ (None, 26, 26, 32) │ 320 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ max_pooling2d (MaxPooling2D) │ (None, 13, 13, 32) │ 0 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ conv2d_1 (Conv2D) │ (None, 12, 12, 16) │ 2,064 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ max_pooling2d_1 (MaxPooling2D) │ (None, 6, 6, 16) │ 0 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ flatten (Flatten) │ (None, 576) │ 0 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ dense (Dense) │ (None, 128) │ 73,856 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ dense_1 (Dense) │ (None, 64) │ 8,256 │
## ├───────────────────────────────────┼──────────────────────────┼───────────────┤
## │ dense_2 (Dense) │ (None, 10) │ 650 │
## └───────────────────────────────────┴──────────────────────────┴───────────────┘
## Total params: 85,146 (332.60 KB)
## Trainable params: 85,146 (332.60 KB)
## Non-trainable params: 0 (0.00 B)
Entraîner et évaluer les performances de votre modèle
La première étape est de compiler l'objet créé précédemment, en définissant l'optimizer qui sera utilisé, la fonction de perte et la métrique sur laquelle on souhaite optimiser le résultat du modèle :
compile(my_first_r_cnn,
optimizer = 'adam',
loss = 'categorical_crossentropy',
metrics = 'accuracy')
Ensuite, on peut lancer l'entraînement avec une instruction fit() que l'on applique à nos données d'entraînement. On y définit notamment le paramètre batch_size qui permet de déterminer combien d'images le modèle va traiter avant d'ajuster ses coefficients. Le paramètre epochs définit le nombre de fois où le modèle passe sur toutes les données. Enfin, on split nos données d'entraînement dont on conserve 30% comme données de validation afin de d'évaluer correctement les performances de notre modèle :
history <- my_first_r_cnn %>% fit(
x_train, y_train,
epochs = 30,
batch_size = 64,
validation_split = 0.3)
## Epoch 1/30
## 657/657 - 5s - 8ms/step - accuracy: 0.9120 - loss: 0.2766 - val_accuracy: 0.9623 - val_loss: 0.1200
## Epoch 2/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9766 - loss: 0.0753 - val_accuracy: 0.9774 - val_loss: 0.0733
## Epoch 3/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9849 - loss: 0.0507 - val_accuracy: 0.9799 - val_loss: 0.0608
## Epoch 4/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9878 - loss: 0.0395 - val_accuracy: 0.9832 - val_loss: 0.0553
## Epoch 5/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9895 - loss: 0.0316 - val_accuracy: 0.9859 - val_loss: 0.0490
## Epoch 6/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9923 - loss: 0.0234 - val_accuracy: 0.9826 - val_loss: 0.0640
## Epoch 7/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9929 - loss: 0.0207 - val_accuracy: 0.9855 - val_loss: 0.0533
## Epoch 8/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9946 - loss: 0.0165 - val_accuracy: 0.9866 - val_loss: 0.0507
## Epoch 9/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9941 - loss: 0.0165 - val_accuracy: 0.9835 - val_loss: 0.0632
## Epoch 10/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9960 - loss: 0.0123 - val_accuracy: 0.9870 - val_loss: 0.0501
## Epoch 11/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9958 - loss: 0.0123 - val_accuracy: 0.9853 - val_loss: 0.0613
## Epoch 12/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9965 - loss: 0.0103 - val_accuracy: 0.9872 - val_loss: 0.0570
## Epoch 13/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9968 - loss: 0.0095 - val_accuracy: 0.9871 - val_loss: 0.0544
## Epoch 14/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9970 - loss: 0.0082 - val_accuracy: 0.9871 - val_loss: 0.0583
## Epoch 15/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9972 - loss: 0.0091 - val_accuracy: 0.9867 - val_loss: 0.0624
## Epoch 16/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9988 - loss: 0.0043 - val_accuracy: 0.9871 - val_loss: 0.0623
## Epoch 17/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9976 - loss: 0.0070 - val_accuracy: 0.9857 - val_loss: 0.0693
## Epoch 18/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9970 - loss: 0.0096 - val_accuracy: 0.9853 - val_loss: 0.0693
## Epoch 19/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9983 - loss: 0.0051 - val_accuracy: 0.9862 - val_loss: 0.0690
## Epoch 20/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9988 - loss: 0.0040 - val_accuracy: 0.9882 - val_loss: 0.0612
## Epoch 21/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9983 - loss: 0.0054 - val_accuracy: 0.9881 - val_loss: 0.0596
## Epoch 22/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9986 - loss: 0.0042 - val_accuracy: 0.9789 - val_loss: 0.1290
## Epoch 23/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9976 - loss: 0.0074 - val_accuracy: 0.9876 - val_loss: 0.0682
## Epoch 24/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9996 - loss: 0.0017 - val_accuracy: 0.9879 - val_loss: 0.0690
## Epoch 25/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9996 - loss: 0.0016 - val_accuracy: 0.9843 - val_loss: 0.0981
## Epoch 26/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9970 - loss: 0.0094 - val_accuracy: 0.9863 - val_loss: 0.0723
## Epoch 27/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9985 - loss: 0.0049 - val_accuracy: 0.9884 - val_loss: 0.0659
## Epoch 28/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9994 - loss: 0.0019 - val_accuracy: 0.9879 - val_loss: 0.0725
## Epoch 29/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9997 - loss: 9.4193e-04 - val_accuracy: 0.9889 - val_loss: 0.0674
## Epoch 30/30
## 657/657 - 1s - 2ms/step - accuracy: 0.9971 - loss: 0.0086 - val_accuracy: 0.9856 - val_loss: 0.0672
On peut illustrer l'évolution de la qualité du modèle au fur et à mesure des epochs avec plot :
plot(history)
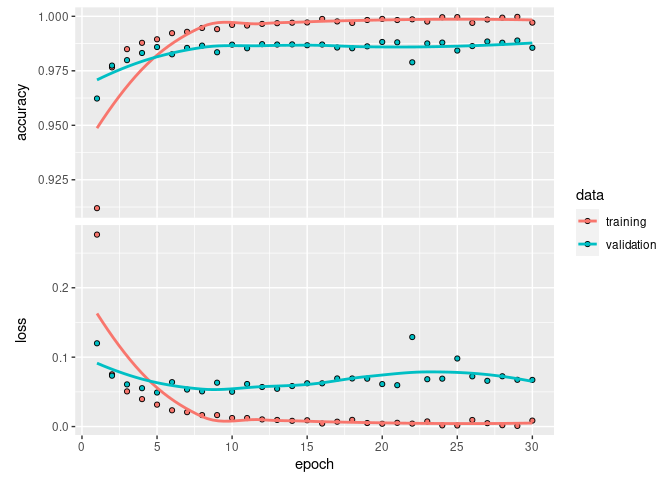
Enfin, on sort la performance du modèle sur nos données test avec evaluate:
accuracy_test <- my_first_r_cnn |> evaluate(x_test, y_test)
## 313/313 - 1s - 3ms/step - accuracy: 0.9898 - loss: 0.0522
print(accuracy_test)
## $accuracy
## [1] 0.9898
##
## $loss
## [1] 0.05221168
Inutile bien sûr de préciser que nous sommes dans un cas de classification relativement simple et avec énormément de données de bonne qualité, donc ne cherchez pas à atteindre de tels niveaux de précision sur des données un peu plus compliquées!
Prédictions à partir du modèle pré-entraîné
Prenons par exemple la 20e image de l'échantillon test :
index <- 20 # On prend la 20e image"
image_data <- x_test[index,,] # Sélection de l'image
label <- mnist$test$y[index] # Label associé
# Inverser les couleurs pour un affichage correct
image_data <- t(apply(image_data, 2, rev))
# Afficher l'image en niveaux de gris
image(image_data, col = gray((0:255)/255),
main = paste("Label :", label),
axes = FALSE, asp = 1)
On peut sortir les prédictions des probabilités associées à chaque classe avec la fonction predict(). La prédiction associée à l'image précédente donne le résultat suivant :
# On prédit l'ensemble des X_test
matrice_pred <- my_first_r_cnn |> predict(x_test)
## 313/313 - 1s - 2ms/step
# On sort l'index max - 1 (qui correspond à la classe) de l'observation n°20
pred_obs <- which.max(matrice_pred[20,]) - 1
image(image_data, col = gray((0:255)/255),
main = paste("Label :", label, "Prédiction :", pred_obs),
axes = FALSE, asp = 1)
Deep Learning avec R ou Python?
Le package keras3 est très complet et semble offrir autant de possibilités que le module Python. Il dispose aussi d'une documentation complète et très détaillée. Cependant, il faut garder en tête qu'il fait tourner Python en arrière-plan.
Le gros avantage pour un utilisateur non aguerri de Python est qu'il va gérer pour vous l'environnement anaconda et les dépendances, qui peuvent être un vrai casse-tête quand on se met à Python. Enfin, la syntaxe très proche de celle de Python peut vous permettre de commencer à vous accoutumer en vue d'un futur changement de langage, tout en restant sur votre langage favori en attendant!
Enfin, on peut imaginer que l'utilisation d'un package R peut être très pratique dans le cadre de la mise en oeuvre de méthodes de statistiques inférentielles sur des prédictions de modèles de Machine Learning, comme par exemple dans ce papier très intéressant.
C'est la fin de cet article! N'hésitez pas à visiter notre site et à nous suivre sur BlueSky et Linkedin. Pour retrouver l'ensemble du code ayant servi à générer cette note, vous pouvez vous rendre sur le github de Statoscop.