Les séries temporelles avec Python (2/4) - Visualisations et opérations sur les séries temporelles
Cet article est le second de notre série sur les données temporelles :
- Introduction à la manipulation de données temporelles avec Python
- Visualisations et opérations sur les séries temporelles
- Éléments théoriques et exemples
- Analyse, modélisation et prédiction
Il s'intéresse dans un premier temps à la visualisation et aux opérations que l'on peut effectuer sur ces objets avant de conclure sur un petit exemple en utilisant les outils présentés dans ces 2 premiers posts.
Un peu d'anglicisme : Resampling, Shifting, and Windowing
- Resampling = rééchantillonnage
- Shifting = déplacement
- Windowing = fenêtrage
La capacité à utiliser les dates/times comme indices pour organiser et accéder aux données est le fondement des outils de séries temporelles sur Pandas. Les avantages de l'indexation (alignement, slicing, etc...) sont conservés et Pandas fournit par ailleurs plusieurs opérations spécifiques aux séries temporelles.
On va donc développer ici quelques unes de ces opérations merveilleuses en utilisant comme premier exemple le cours de l'action Google en bourse (données récupérées sur Yahoo finance).
Petite précision en passant, le terme "séries temporelles" désigne en général, dans le contexte Pandas, un objet Series indexé par un DatetimeIndex.
import pandas as pd
# parse_dates=True permet à pandas de repérer les dates sous différents formats
goog = pd.read_csv('data/GOOG.csv', index_col='Date', parse_dates=True)
goog.head(2)
| Open | High | Low | Close | Adj Close | Volume | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2004-08-19 | 49.813290 | 51.835709 | 47.800831 | 49.982655 | 49.982655 | 44871361 |
| 2004-08-20 | 50.316402 | 54.336334 | 50.062355 | 53.952770 | 53.952770 | 22942874 |
goog.tail(2)
| Open | High | Low | Close | Adj Close | Volume | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2021-05-21 | 2365.98999 | 2369.00000 | 2342.370117 | 2345.100098 | 2345.100098 | 1139600 |
| 2021-05-24 | 2367.00000 | 2418.47998 | 2360.110107 | 2406.669922 | 2406.669922 | 1061400 |
Ces données recensent certaines informations sur l'action Google du 19 août 2004 au 24 mai 2021 : les prix à l'ouverture et à la clôture, le maximum et le minimum sur la journée, les prix ajustés et les volumes. On étudie ici la série temporelle des prix à la clôture.
goog = goog['Close']
goog.index
DatetimeIndex(['2004-08-19', '2004-08-20', '2004-08-23', '2004-08-24',
'2004-08-25', '2004-08-26', '2004-08-27', '2004-08-30',
'2004-08-31', '2004-09-01',
...
'2021-05-11', '2021-05-12', '2021-05-13', '2021-05-14',
'2021-05-17', '2021-05-18', '2021-05-19', '2021-05-20',
'2021-05-21', '2021-05-24'],
dtype='datetime64[ns]', name='Date', length=4220, freq=None)
C'est bien une série indexée par un DatetimeIndex que l'on affiche avec style en fixant les paramètres d'affichage par défaut comme étant ceux de seaborn :
import matplotlib.pyplot as plt
import seaborn as sns ; sns.set() #pour définir les paramètres d'affichage de seaborn par défaut
plt.rcParams["figure.figsize"] = (12,8)
goog.plot();
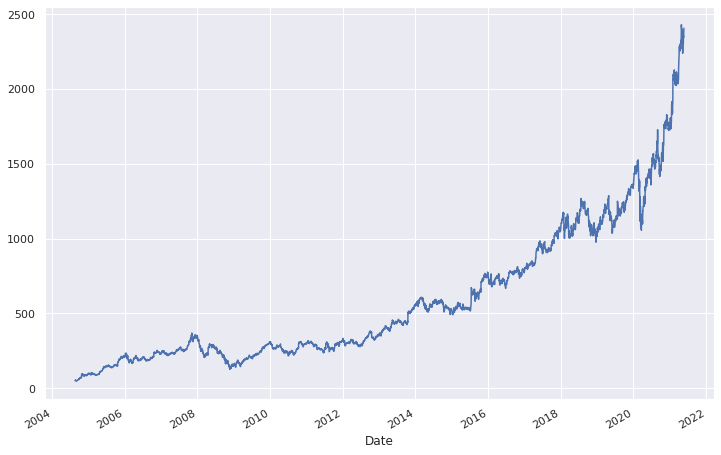
Rééchantillonage et conversion de fréquences
Une manipulation classique des séries temporelles est le rééchantionnage (resampling) à une fréquence plus ou moins haute. Cela consiste à augmenter ou diminuer la fréquence des observations. Il y a donc 2 possibilités :
- si on augmente la fréquence cela veut dire ajouter des points et dans ce cas il faut définir quelle stratégie utiliser pour interpoler les nouveaux points (un exemple de stratégie basique est de répéter la dernière valeur) ;
- si on diminue la fréquence, ce qui est le cas le plus classique, on va supprimer des points et il faut là aussi déterminer la stratégie à utiliser. Deux options sont possibles : on sélectionne uniquement les points correspondants à la nouvelle fréquence plus faible ou bien on agrège les points entre 2 fréquences en utilisant une fonction d'aggrégation comme par exemple une moyenne, une médiane, un max, etc...
Pour ce faire, pandas dispose de deux méthodes qui sont resample() ou asfreq(). La différence entre les deux est que resample consiste à agréger toutes les données comprises entre 2 multiples de la fréquence alors que asfreq sélectionne la valeur correspondant à la fréquence. Aussi, resample renvoie un objet particulier qui est un DatetimeIndexResampler sur lequel il faut appliquer une méthode d'aggrégation ou d'imputation pour récupérer une série. La méthode asfreq retourne directement une série.
On va de ce pas illustrer avec la série Google en diminuant la fréquence afin de n'avoir qu'un point par année. On va prendre le dernier jour ouvrable de l'année (jour ouvrable car la série prend des valeurs uniquement pour les jours ouvrables).
Petit rappel, on utilise ci-dessous, le code de fréquence BA pour récupérer le dernier jour ouvrable de l'année mais pour en savoir plus sur les fréquences, l'épisode 1 de cette série vous en apprendra davantage.
goog.plot(alpha=0.4)
goog.resample('BA').mean().plot()
goog.asfreq('BA').plot();
plt.legend(['close', 'resample', 'asfreq'], loc='upper left');
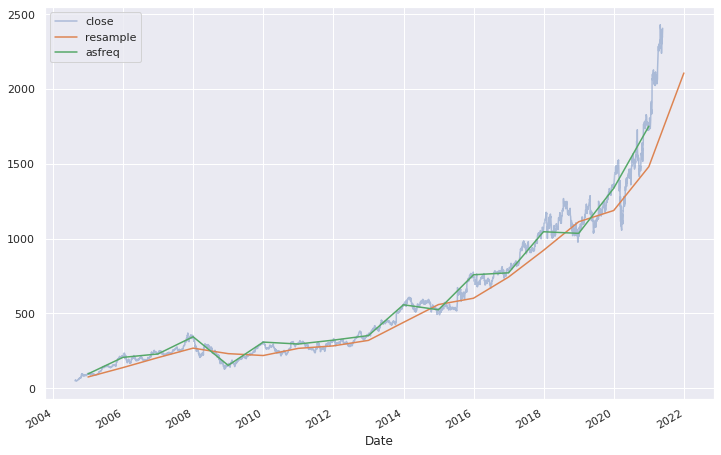
Pour un resampling avec une fréquence plus importante, resample() et asfreq() sont équivalentes. Par défaut, les 2 méthodes laissent les valeurs non existantes vides. Toutefois, asfreq() accepte un paramètre method dans lequel on peut spécifier comment imputer les valeurs manquantes générées par l'augmentation de la fréquence. C'est faisable aussi avec resample en utilisant les méthodes bfill ou ffill des objets pandas.core.resample.Resampler.
Le petit bout de code ci-dessous selectionne uniquement les 14 derniers jours et effectue un resampling de la série avec une fréquence quotidienne (cela inclue donc les weekends !). Ensuite on affiche pour chaque méthode (resample() et asfreq()) les courbes rééchantillonnées sans imputer les valeurs manquantes, avec une imputation de type bfill qui impute la première valeur suivante non manquante (donc dans ce cas celle du lundi) et de type ffill qui impute la dernière valeur (donc ici, celle du vendredi).
data = goog.iloc[-14:]
#visualisation
fig, ax = plt.subplots(2,2, sharex=True, sharey=True, figsize=(14,9))
#avec asfreq
data.asfreq('D').plot(ax=ax[0,0], marker='o')
ax[0,0].set_title("asfreq()", fontsize=20);
data.asfreq('D', method='bfill').plot(ax=ax[1,0], style='-o')
data.asfreq('D', method='ffill').plot(ax=ax[1,0], style='--o')
ax[1,0].legend(["back-fill", "forward-fill"]);
#avec resample
data.resample('D').mean().plot(ax=ax[0,1], marker='o')
ax[0,1].set_title("resample()", fontsize=20);
data.resample('D').bfill().plot(ax=ax[1,1], style='-o')
data.resample('D').ffill().plot(ax=ax[1,1], style='--o')
ax[1,1].legend(["back-fill", "forward-fill"]);
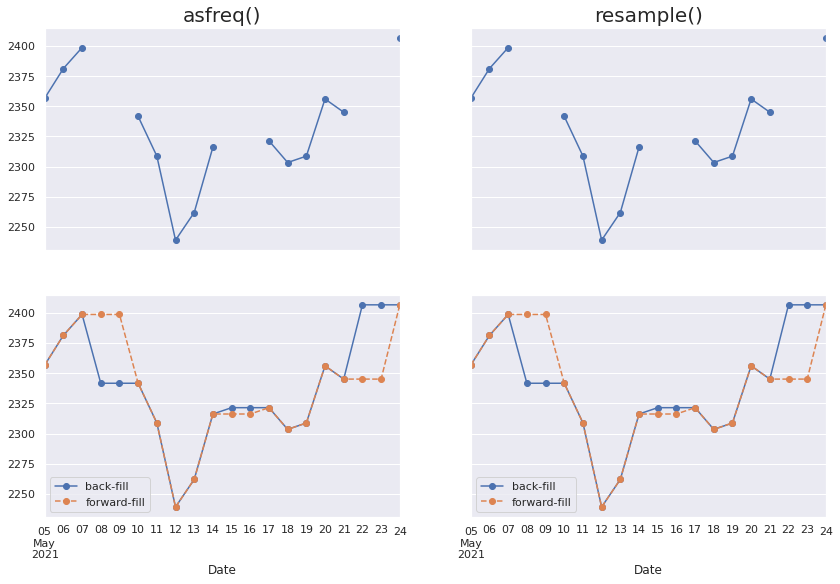
Déplacements
Une autre opération fondamentale de l'analyse des données temporelles est le déplacement ou décalage (on parle plus souvent de time-shifts ou shifting)
On utilise pour cette opération la méthode shift() dont le principe est de déplacer les valeurs par rapport aux indices. Le décalage doit bien sûr être un multiple de la fréquence !
fig, ax = plt.subplots(3, sharey=True)
goog = goog.asfreq('D', method='ffill')
goog.plot(ax=ax[0])
goog.shift(900).plot(ax=ax[1])
goog.shift(-900).plot(ax=ax[2])
local_max = pd.to_datetime('2010-01-01')
offset1 = pd.Timedelta(900, 'D')
offset2 = pd.Timedelta(-900, 'D')
ax[0].legend(['close'], loc=2)
ax[0].get_xticklabels()[3].set(weight='heavy', color='red')
ax[0].axvline(local_max, alpha=0.3, color='red')
ax[1].legend(['shift(900)'], loc=2)
ax[1].get_xticklabels()[3].set(weight='heavy', color='red')
ax[1].axvline(local_max + offset1, alpha=0.3, color='red')
ax[2].legend(['shift(-900)'], loc=2)
ax[2].get_xticklabels()[3].set(weight='heavy', color='red')
ax[2].axvline(local_max + offset2, alpha=0.3, color='red');
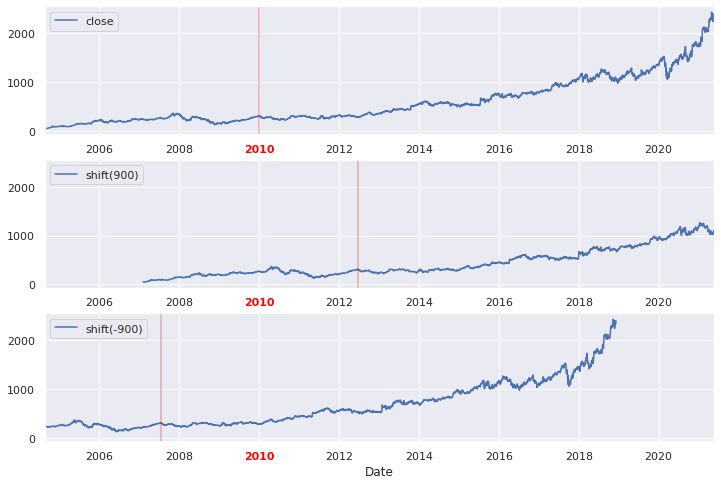
Une utilisation possible du shifting est par exemple de calculer le retour sur investissement à 1 an de l'action de Google (ROI - return on investment, par ici Wiki).
ROI_1 = 100 * (goog.shift(-365) / goog - 1)
ROI_1.iloc[:-365].plot()
plt.ylabel('ROI');
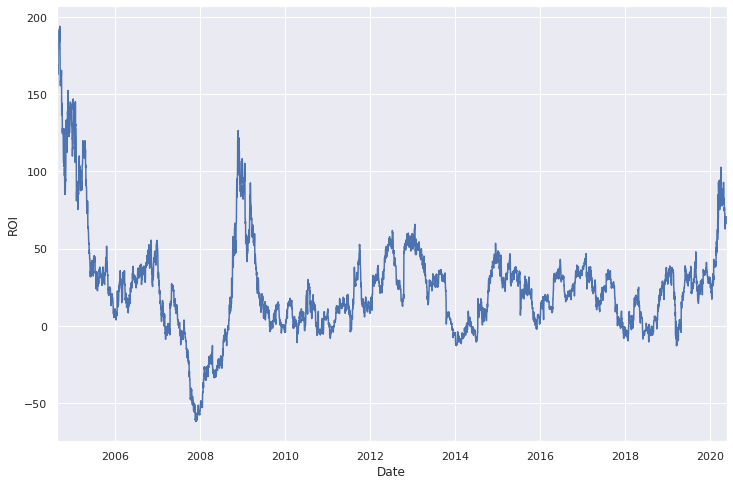
Qu'en conclure ? Pour les boursicoteurs, vous avez raté le coche, fallait acheter en 2004 ou en 2009.
Attention, fenêtres glissantes
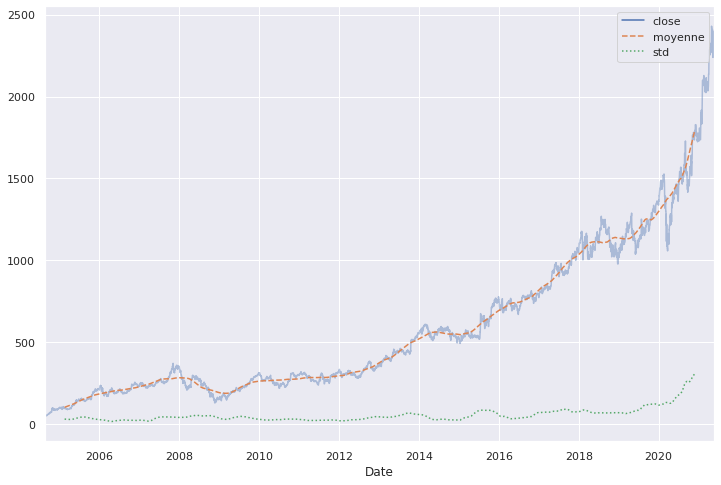
Enfin, la 3ème opération classique des séries temporelles consiste à calculer différentes statistiques sur une fenêtre d'une longueur donnée et qui se déplace. On parle plus de rolling window que de fenêtres glissantes...et pour ce faire, Pandas a tout ce qu'il faut avec la méthode rolling() pour les objets Series et DataFrame. Regardons d'un peu plus près en calculant avec la méthode rolling la moyenne annuelle centrée et l'écart-type annuel centré.
rol = goog.rolling(365, center=True)
data = pd.DataFrame({'close': goog,
'moyenne': rol.mean(),
'std': rol.std()})
ax = data.plot(style=['-', '--', ':'])
ax.lines[0].set_alpha(0.4)
👋 Nous c'est Antoine et Louis de Statoscop, une coopérative de statisticiens / data scientists. Vous voulez en savoir plus sur ce que l'on fait?
Un exemple de visualisation : le nombre de vélos à Paris Montparnasse
On va terminer sur un petit exemple un peu plus parlant, ou en tout cas, un peu moins financier, en regardant le nombre de vélos passés devant un des compteurs de la ville de Paris, situé sur le boulevard Montparnasse. Le jeu de données vient de là. On récupère ainsi le décompte horaire des vélos.
Nettoyage des données
Un premier coup d'oeil sur les données nous permet de voir qu'il y a beaucoup de colonnes inutiles dans ce dataset. On va donc se contenter de ce qui nous intéresse : le timestamp et le nombre de vélos. Avec un petit peu de nettoyage directement au moment de l'import dans le pandas.read_csv, ça donne :
velo = pd.read_csv('data/comptage-velo-donnees-compteurs.csv', sep=';',
names=["nb", "date"], header=0,
usecols=[4,5])
velo.head(3)
| nb | date | |
|---|---|---|
| 0 | 21.0 | 2020-04-01T07:00:00+02:00 |
| 1 | 21.0 | 2020-04-01T09:00:00+02:00 |
| 2 | 14.0 | 2020-04-01T12:00:00+02:00 |
En important le jeu de données, on voit ce "+02:00" qui définit en fait la timezone. Plusieurs solutions possibles pour gérer ce problème :
- on peut utiliser les méthodes de manipulation de timezone avec tz_convert et tz_localize
- on peut définir notre propre parser de date au moment de l'import en supprimant le "+02:00" avec un split par exemple.
Ci-dessous, ces 2 approches mises en oeuvre.
pd.DatetimeIndex(pd.to_datetime(velo.date, utc=True)).tz_convert('Europe/Paris').tz_localize(None)
DatetimeIndex(['2020-04-01 07:00:00', '2020-04-01 09:00:00',
'2020-04-01 12:00:00', '2020-04-01 15:00:00',
'2020-04-01 16:00:00', '2020-04-01 19:00:00',
'2020-04-01 20:00:00', '2020-04-01 21:00:00',
'2020-04-01 22:00:00', '2020-04-01 23:00:00',
...
'2021-05-22 20:00:00', '2021-05-23 00:00:00',
'2021-05-23 02:00:00', '2021-05-23 03:00:00',
'2021-05-23 04:00:00', '2021-05-23 16:00:00',
'2021-05-23 19:00:00', '2021-05-24 02:00:00',
'2021-05-24 05:00:00', '2021-05-24 14:00:00'],
dtype='datetime64[ns]', name='date', length=10046, freq=None)
velo = pd.read_csv('data/comptage-velo-donnees-compteurs.csv', sep=';',
names=["nb", "date"], header=0,
usecols=[4,5],
index_col="date",
parse_dates=True,
date_parser=lambda s: pd.to_datetime(s.split("+")[0])
)
# read_csv retourne un dataframe or on veut un objet Series, donc puisqu'on le veut, et qu'on l'a, ben on le prend.
velo = velo.nb
velo[:3]
date
2020-04-01 07:00:00 21.0
2020-04-01 09:00:00 21.0
2020-04-01 12:00:00 14.0
Name: nb, dtype: float64
Regardons à quoi ressemble cette série temporelle du nombre de vélos sur le boulevard Montparnasse !
velo.plot(legend=False)
plt.ylabel('Décompte horaire des vélos');
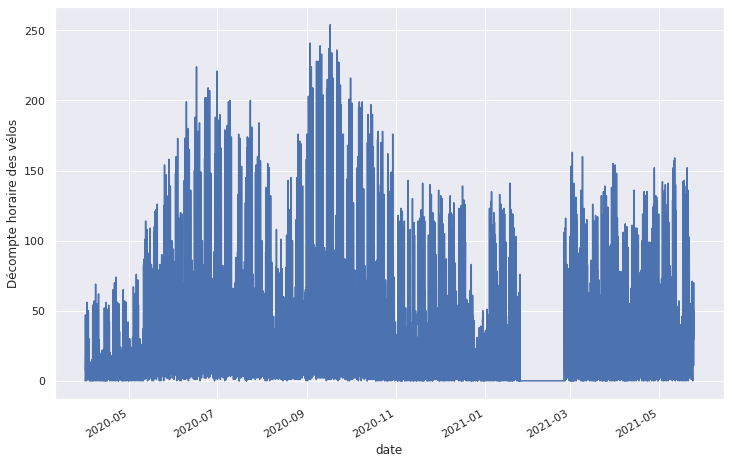
On voit pas grand chose pour le moment mais on détecte déjà un problème de valeurs manquantes au niveau du mois de février 2021. On va donc prendre les données de 2020 uniquement pour s'épargner la gestion de ces données manquantes.
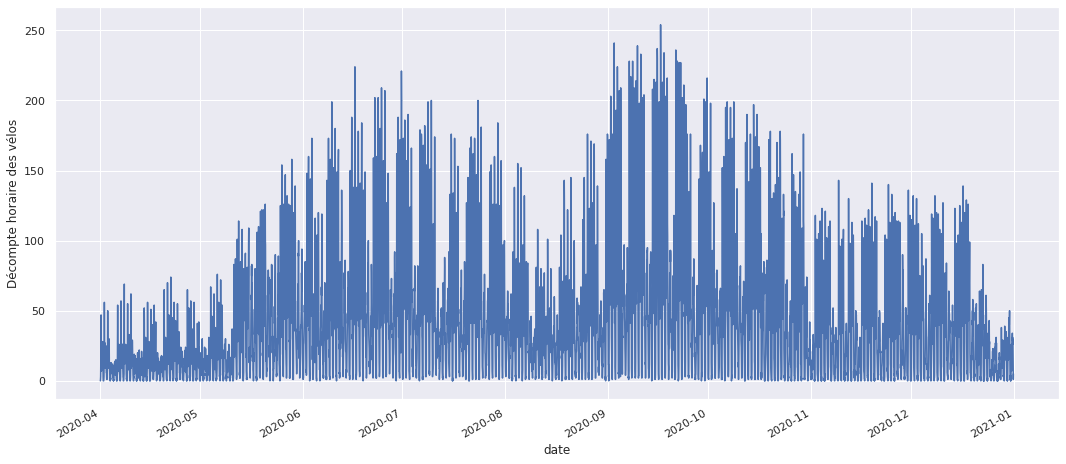
velo = velo['2020']
velo.plot(legend=False, figsize=(18,8))
plt.ylabel('Décompte horaire des vélos');
Analyse des données
La série par heure étant trop "dense" pour être clairement lisible, on va diminuer la fréquence avec un resample pour faire la somme des vélos sur une journée et sur une semaine.
fig, ax = plt.subplots(1,2,figsize=(18,7))
# Somme sur une journée
velo_jr = velo.resample('D').sum()
velo_jr.plot(ax=ax[0], legend=False)
ax[0].set_ylabel('Décompte journalier des vélos');
# Somme sur une semaine
velo_sem = velo.resample('W').sum()
velo_sem.plot(ax=ax[1], legend=False)
ax[1].set_ylabel('Décompte hebdo des vélos');
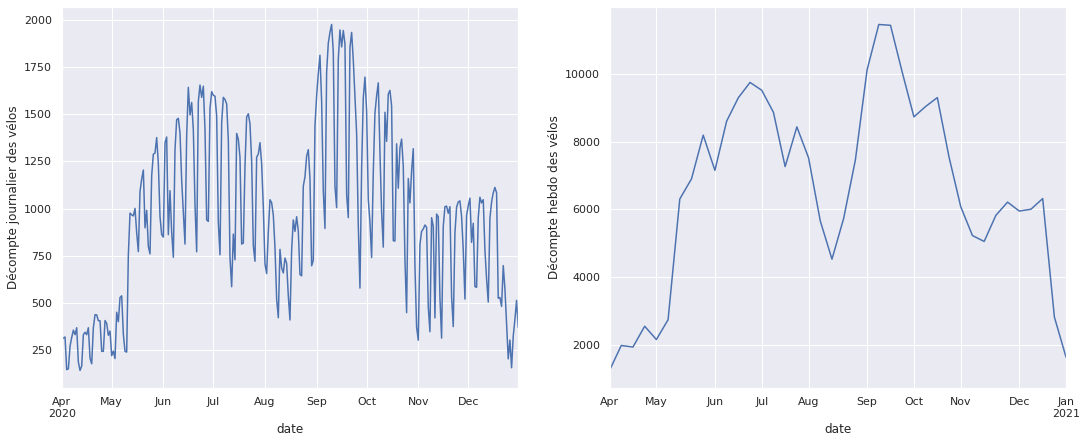
Avec ces rééchantillonages on veut une tendance annuelle qui se dégage avec notamment un pic de reprise d'activité au printemps, après le confinement et une baisse de fréquentation pendant l'été. De la même manière, la baisse significative visible au mois de novembre est certainement dûe au second confinement de 2020.
Une autre information visible sur le graphique des décomptes journaliers est la baisse du nombre de vélo environ 4 fois par mois, cela correspond certainement aux weekends mais ne nous avançons pas trop...
On va regarder avec la méthode rolling, la moyenne mobile mensuelle et faire jouer certains paramètres afin de voir ce qu'il en est.
plt.figure(figsize=(20,12))
plt.plot(velo_jr.rolling(30, center=True).mean(),label="unweighted")
for std in [1,5,10,15,20,30]:
plt.plot(velo_jr.rolling(30, center=True, win_type='gaussian').mean(std=std), label=f"win{std}")
plt.legend(loc='best');
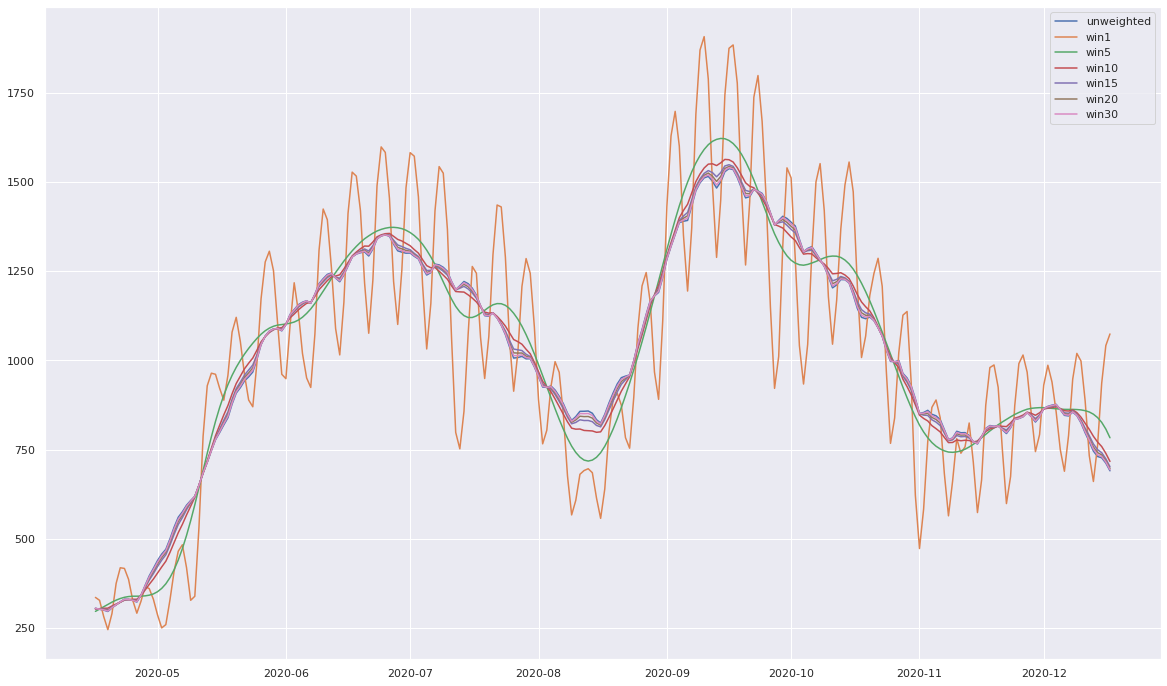
Le paramètre win_type="gaussian" permet d'appliquer une pondération au calcul de la moyenne. En l'occurence on applique des poids qui suivent une loi normale dont l'écart-type est défini dans la fonction d'aggrégation mean. Plus cet écart-type est faible, plus les jours proches comptent et ceux éloignés ne comptent pas. C'est le cas de la courbe orange qui a donc tendance à suivre d'assez près la courbe initiale. En revanche, si l'on augmente l'écart-type, on prend en compte plus de jours autour et on lisse ainsi les résultats. Pour finir, si l'écart-type est très élevé, alors on pondère de manière quasi identique les 30 jours de la fenêtre et on retombe donc sur une moyenne non-pondérée.
On va regarder maintenant comment ça se passe au niveau hebdomadaire pour comprendre comment évolue la fréquentation selon les différents horaires d'une journée et selon les différents jours d'une semaine. Pour cela, on va pouvoir utiliser les attributs time et dayofweek des objets DatetimeIndex afin d'afficher les décomptes de vélos par heure de la journée et par jour de la semaine.
import numpy as np
fig, ax = plt.subplots(1,2,figsize=(18,7))
par_hr = velo.groupby(velo.index.time).mean()
heures = 4 * 60 * 60 * np.arange(6)
par_hr.plot(ax=ax[0], xticks=heures, legend=False);
par_sem = velo.groupby(velo.index.dayofweek).mean()
par_sem.index = ['Lundi', 'Mardi', 'Mercredi', 'Jeudi', 'Vendredi', 'Samedi', 'Dimanche']
par_sem.plot(ax=ax[1], legend=False);
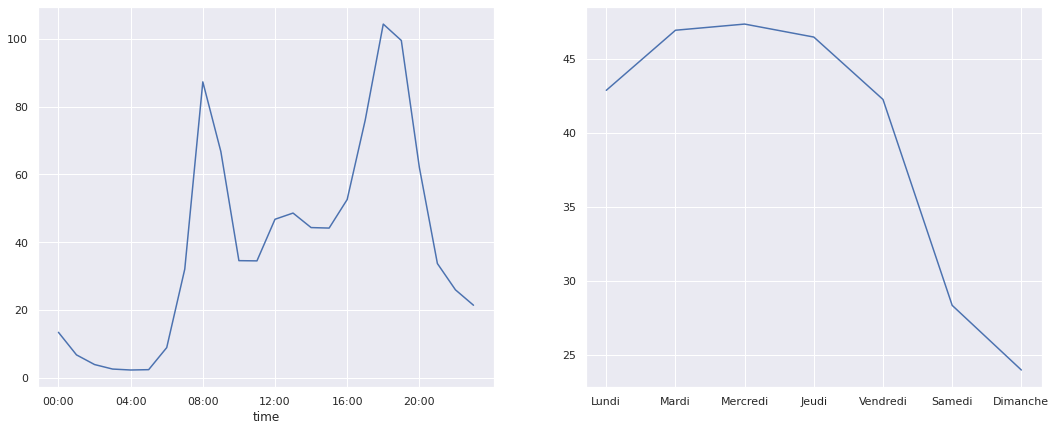
On retrouve bien certaines informations qu'on avait évoquées :
- baisse de la fréquentation le weekend et sur une journée,
- pics de fréquentation à 8h et à 18h et légère augmentation à l'heure du déjeuner.
Cette 2ème information est certes logique pour les jours ouvrables mais c'est plus étonnant pour les jours de weekends...allons voir de plus près !
jours_ouvrables = np.where(velo.index.dayofweek < 5, 'Ouvrable', 'Weekend')
par_hr = velo.groupby([jours_ouvrables, velo.index.time]).mean()
fig, ax = plt.subplots(1,2,figsize=(18,7))
par_hr.loc['Ouvrable'].plot(ax=ax[0], title='Jours ouvrables', xticks=heures, legend=False)
par_hr.loc['Weekend'].plot(ax=ax[1], title='Weekends', xticks=heures, legend=False);
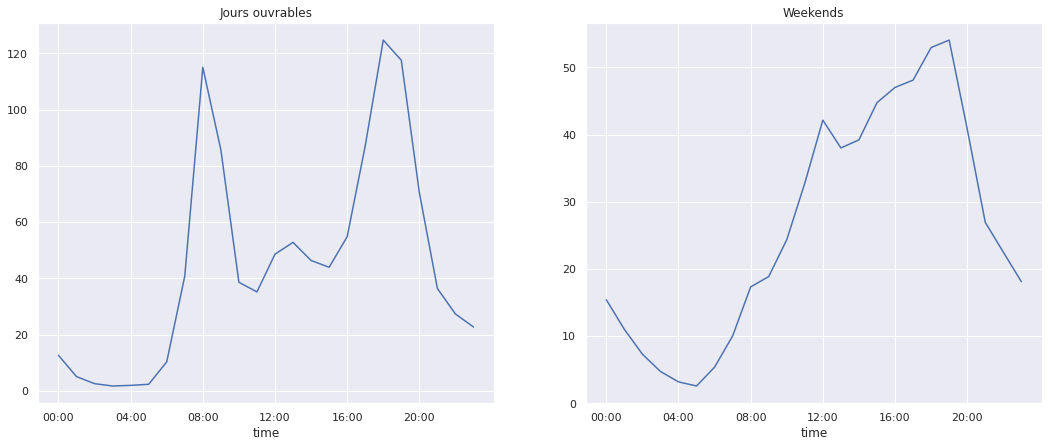
C'est tout de suite plus clair : le weekend, les gens dorment et sortent se promener l'après-midi ! Nous voilà rassurés. Sur cette belle découverte, on se dit à très vite pour le post numéro 3 de cette série ! Comme d'habitude, vous pouvez retrouver l'ensemble du notebook ayant servi à générer cette note sur le github de Statoscop.